最短経路問題
ベルマンフォード法とワーシャルフロイド法について解説します。 ダイクストラ法と比べて構造が単純(プライオリティキューがいらない)なので、多少は理解しやすいと思います。
入力の形式について
このページで使用しているサンプルコードの標準入力は、全て下記の形式で与えられます。
n m $$[f_1 \ t_1 \ c_1]$$ $$[f_2 \ t_2 \ c_2]$$ ... $$[f_m \ t_m \ c_m]$$
nは頂点数、mは辺の数を示し、続くm行の \([f\_i, t\_i, c\_i]\) はそれぞれi番目の辺の始点、終点、重みを示します。
ベルマンフォード法
ベルマンフォード法は、2点間の最短路を見つけるアルゴリズム。
ダイクストラ法はうまく頂点を選ぶことで効率を上げているが、ベルマンフォード法では全ての辺に対して距離が短くなる経路があるか判定する。
基本的には、ベルマンフォード法はダイクストラ法より遅い。計算量は、辺の数をE、頂点数をVとすると、O(EV)となる。
ただし、ベルマンフォード法は負の辺があっても正しく動作し、負の閉路を検出することができる。負の閉路があると、その閉路内をずっと回っていれば無限に距離を減らすことができてしまい、ダイクストラ法では無限ループor誤った答えを返す。
また、距離が確定した頂点を選ぶ操作が不要なので、コードも多少単純化される。
以下のコードはベルマンフォード法の実装です。グラフは隣接リスト形式で表現されています(グラフの表現方法については後述)。
#include <iostream>
#include <vector>
using namespace std;
// 隣接リストで使う辺を表す型
struct Edge {
int to, cost; // 辺の接続先頂点, 辺の重み
Edge(int to, int cost) : to(to), cost(cost) {} // コンストラクタ
};
typedef vector<vector<Edge> > AdjList; // 隣接リストの型
AdjList graph; // グラフの辺を格納した構造体
// graph[v][i]は頂点vから出るi番目の辺Edge
const int INF = 100000000;
vector<int> dist; // 最短距離
// 戻り値がtrueなら負の閉路を含む
bool bellman_ford(int n, int s) { // nは頂点数、sは開始頂点
dist = vector<int>(n, INF);
dist[s] = 0; // 開始点の距離は0
for (int i = 0; i < n; i++) {
for (int v = 0; v < n; v++) {
for (int k = 0; k < graph[v].size(); k++) {
Edge e = graph[v][k];
if (dist[v] != INF && dist[e.to] > dist[v] + e.cost) {
dist[e.to] = dist[v] + e.cost;
if (i == n - 1) return true; // n回目にも更新があるなら負の閉路が存在
}
}
}
}
return false;
}
int main() {
int n, m;
cin >> n >> m;
graph = AdjList(n);
for (int i = 0; i < m; i++) {
int from, to, cost;
cin >> from >> to >> cost;
graph[from].push_back(Edge(to, cost));
}
bellman_ford(n, 0);
for (int i = 1; i < n; i++) {
if (dist[i] != INF)
cout << "0から" << i << "へのコスト: " << dist[i] << endl;
}
return 0;
}以下は同アルゴリズムを隣接行列で実装したものです(講習会のときはこちらのコードのみ掲載していました)。計算量は \([O(V^3)]\) で、辺の数Eが小さなグラフに対しては隣接リストを使った場合よりも効率が悪いです。
#include <iostream>
#include <vector>
using namespace std;
typedef vector<vector<int> > Matrix;
const int INF = 100000000;
Matrix graph; // グラフの距離を格納した2次元配列(隣接行列)
// graph[u][v]は辺e=(u,v)のコスト(辺が存在しない場合はINF)
vector<int> dist; // 最短距離
// 戻り値がtrueなら負の閉路を含む
bool bellman_ford(int n, int s) { // nは頂点数、sは開始頂点
dist = vector<int>(n, INF);
dist[s] = 0; // 開始点の距離は0
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
if (j == k) continue;
int cost = graph[j][k];
if (dist[j] != INF && dist[k] > dist[j] + cost) {
dist[k] = dist[j] + cost;
if (i == n - 1) return true; // n回目にも更新があるなら負の閉路が存在
}
}
}
}
return false;
}
int main() {
int n, m;
cin >> n >> m;
graph = Matrix(n, vector<int>(n, INF));
for (int i = 0; i < m; i++) {
int from, to, cost;
cin >> from >> to >> cost;
graph[from][to] = cost;
}
bellman_ford(n, 0);
for (int i = 1; i < n; i++) {
if (dist[i] != INF)
cout << "0から" << i << "へのコスト: " << dist[i] << endl;
}
return 0;
}入力例:
4 4
0 1 2
0 2 3
0 3 100
2 3 4入力例に対応するグラフ:
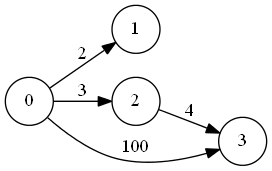
出力例:
0から1へのコスト: 2
0から2へのコスト: 3
0から3へのコスト: 7
ワーシャルフロイド法
ワーシャルフロイド法は、グラフの全ての頂点の間の最短路を見つけるアルゴリズム。
「3つの頂点a, b, cを選んで、a→b→cという道がa→cという道より短ければa→cの距離を更新する」
という操作を全ての頂点の組み合わせで繰り返して最短距離を確定させていく。(a→b→cやa→cの道が存在しないときは、距離が無限大の道があると考え、a→aのような道は距離0としておく)
これは単純なforループで実現可能。計算量は、頂点数をVとすると\([O(V^3)]\)。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef vector<vector<int> > Matrix;
const int INF = 100000000;
Matrix d; // グラフの距離を格納した2次元配列(隣接行列)
// d[u][v]は辺e=(u,v)のコスト(辺が存在しない場合はINF、ただしd[i][i]=0)
void warshall_floyd(int n) { // nは頂点数
for (int i = 0; i < n; i++) // 経由する頂点
for (int j = 0; j < n; j++) // 開始頂点
for (int k = 0; k < n; k++) // 終端
d[j][k] = min(d[j][k], d[j][i] + d[i][k]);
}
int main() {
int n, m;
cin >> n;
d = Matrix(n, vector<int>(n, INF));
for (int i = 0; i < n; i++) d[i][i] = 0;
cin >> m;
for (int i = 0; i < m; i++) {
int from, to, cost;
cin >> from >> to >> cost;
d[from][to] = cost;
}
warshall_floyd(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i != j && d[i][j] != INF)
cout << i << "から" << j << "へのコスト: " << d[i][j] << endl;
}
}
return 0;
}入力例:
4 6
0 1 10
0 3 100
1 3 1000
2 1 1
2 3 10000
3 0 5入力例に対応するグラフ:
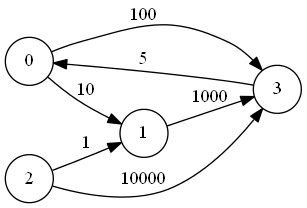
出力例:
0から1へのコスト: 10
0から3へのコスト: 100
1から0へのコスト: 1005
1から3へのコスト: 1000
2から0へのコスト: 1006
2から1へのコスト: 1
2から3へのコスト: 1001
3から0へのコスト: 5
3から1へのコスト: 15
コードが短いので計算時間に余裕があるなら2点間の最短経路に使ってもいいかも。
ちなみに、ワーシャルフロイド法でも負の辺に対応できる。負の閉路があると、d[i][i]が負となる(d[i][i]は負閉路がなければ0になっているはず)。
ワーシャルフロイド法はプログラムは単純だが、なぜこれでうまく最短経路が見つかるのかは理解しづらい。 プログラミングコンテストチャレンジブック(通称蟻本)の98ページに動的計画法を用いた解説があるので、気になる人はそれを参照してください。
演習
補足:グラフをプログラム上で管理する方法
上記にある2つのサンプルコードは、グラフが重み付きの(辺に距離などのデータが付いている)有向グラフで、隣接行列を使ってグラフを表現したときの処理になっている。
グラフを管理する方法は、主に隣接行列と隣接リストの2つの方法がある。
隣接行列は行列を使って辺を管理し、隣接リストは頂点毎に辺を格納して管理する方法のこと。
隣接行列と隣接リストは一長一短で、一般にダイクストラ法とベルマンフォード法は隣接リストを使ったほうが効率がよく、ワーシャルフロイド法は隣接行列を使ったほうが効率がよかったりする。
なので、状況によって使い分ける必要がある(とはいえ多くの場合どちらを使っても大差はなかったり…そんなことありませんでした両者は全然違うので使い分けましょう。巨大なグラフや多重辺を扱う場合は隣接リストでなければならない場合が多いです)。
以下は隣接行列と隣接リストの両方を使ったサンプルコード。入力の形式は上述の通り。
#include <iostream>
#include <vector>
using namespace std;
const int INF = 100000000; // 無限
int n, m; // 頂点数, 辺数
typedef vector<vector<int> > AdjMatrix; // 隣接行列の型
AdjMatrix mat_graph; // 隣接行列表現のグラフを表すグローバル変数
void input_graph_adj_matrix() {
// 隣接行列を生成。INFで辺がないことを表す
mat_graph = AdjMatrix(n, vector<int>(n, INF));
// 場合によっては次のように自己ループ辺の重みを0にする(ワーシャルフロイド法で必要)
// for (int i = 0; i < n; i++) mat_graph[i][i] = 0;
for (int i = 0; i < m; i++) {
int from, to, cost;
cin >> from >> to >> cost;
// cost = 1; // 重みなしグラフならコスト1
mat_graph[from][to] = cost;
// 入力が無向グラフなら次のように逆辺も張る
// mat_graph[to][from] = cost;
}
}
// 隣接リストで使う辺を表す型
struct Edge {
int to, cost; // 辺の接続先頂点, 辺の重み
Edge(int to, int cost) : to(to), cost(cost) {} // コンストラクタ
// 余談だが、コンストラクタを使うと、
// Edge e; e.to=to; e.cost=cost; vec.push_back(e);
// と書くような処理を
// vec.push_back(Edge(to, cost));
// と書けるようになり、若干楽。
};
typedef vector<vector<Edge> > AdjList; // 隣接リストの型
AdjList list_graph; // 隣接リスト表現のグラフを表すグローバル変数
void input_graph_adj_list() {
// 隣接リストを生成
list_graph = AdjList(n);
for (int i = 0; i < m; i++) {
int from, to, cost;
cin >> from >> to >> cost;
list_graph[from].push_back(Edge(to, cost));
// 入力が無向グラフなら逆辺も張る
// list_graph[to].push_back(Edge(from, cost));
}
}
int main() {
cin >> n >> m; // 頂点数, 辺数
if (true) { // 隣接行列を使う場合
input_graph_adj_matrix();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (mat_graph[i][j] != INF)
cout << i << "から" << j << "への辺のコスト: " << mat_graph[i][j] << endl;lkjj
}
}
}
else { // 隣接リストを使う場合
input_graph_adj_list();
for (int i = 0; i < n; i++) {
for (int j = 0; j < list_graph[i].size(); j++) {
cout << i << "から" << list_graph[i][j].to << "への辺のコスト: "
<< list_graph[i][j].cost << endl;
}
}
}
return 0;
}参考文献
プログラミングコンテストチャレンジブック: 秋葉 拓哉, 岩田 陽一, 北川 宜稔