目次

最小全域木（クラスカル法とUnionFind）

今回は無向グラフの最小全域木について説明します。 最小全域木を用いる問題はICPCでもたまに出題されます（今年のアジア地区予選東京大会F問題とか）。

最小全域木とは

無向連結グラフの全域木は、グラフが連結であるという条件を保ったまま辺を消去して得られる木のことです。 最小全域木は、全域木を構成する辺のコストの総和が最小となるもののことを指します。 最小全域木問題は、与えられたグラフの最小全域木またはそのコストを求める問題です。

次の図は最小全域木の例です。赤い辺が最小全域木を構成します。 赤い辺以外を消去するとグラフは全域木になり、また少し考えるとこれよりコストの和が小さい全域木が存在しないことがわかります。

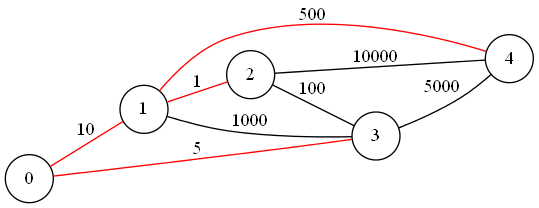
最小全域木の例

最小全域木問題の解法

最小全域木は

という貪欲法で求められます。 このアルゴリズムはクラスカル法と呼ばれます。 クラスカル法で最小全域木が得られることの証明はWikipediaの記事を参照してください。

なお今回は説明しませんが、同種のアルゴリズムとしてプリム法もあります。 これはダイクストラ法に類似したアルゴリズムで、クラスカル法よりも若干効率的です。

クラスカル法

クラスカル法は以下のような疑似コードで実現できます。

foreach 辺e in E in ascending order
  if 採用した辺集合にeを加えても閉路を作らない then eを採用
return 採用した辺のコストの和

辺をコストの小さい順で走査するのは、辺情報を格納した配列を事前にソートすれば簡単に実現できます。 問題はすでに採用済みの辺の集合にeを追加したときに閉路を作るかどうかの判定です。 この判定にはUnion Findというデータ構造を利用します。

Union Find （素集合データ構造）

Union Findは、n個のデータがn個のグループ（集合）のどれかに属しているようなグループ群に対し、

という処理を効率よく行えるデータ構造です。 Union Findにはいくつか種類がありますが、ここでは木構造を用いるものを考えます（以下これを単にUnion Findと呼びます）。

Union Findでは、グループを複数の根付き木からなる森として管理し、データが同じグループに属するなら同じ木に含まれるものとします。 また、2種類の高速化（経路圧縮とデータ構造をマージする一般的なテク）により、グループのマージと同じグループに属するかの判定がほぼ定数時間（逆アッカーマン関数）で行えます。 詳細はプログラミングコンテストチャレンジブックのUnion Find木の項（81ページ）またはプログラミングコンテストでのデータ構造を見てください。

Union Findを用いると、採用済みの辺の集合に新たな辺を追加したときに閉路ができるかどうかの判定が次のように行えます。 採用済みの辺の集合について、グラフのある頂点とある頂点が連結しているならばUnion Findの同じグループに属している、とします。 この時、点i,jを結ぶ新たな辺eを追加しようとしたとき、i,jが同じグループに属するならば、すでにiからjへのパスが存在しているため、eを追加すると閉路ができることがわかります。 逆に同じグループに属しないならば閉路はできないので、その辺を採用することができます。 辺eを採用した際は、頂点i,jに対してunite処理を行えば採用済みの辺の集合を更新することができます。

Union Findの実装

構造体を使った実装です。 データとして0..n-1の整数値を用います。 処理の説明のため若干実装量が多いので、ICPCで使う際はparとsizesを1つの変数に圧縮して実装量を減らすといいと思います（参考：Spaghetti Source - Union Find）。

#include <iostream>
#include <vector>
using namespace std;
#define rep(i,n) for (int i=0; i < int(n); i++)


// 素集合データ構造
struct UnionFind
{
  // par[i]：データiが属する木の親の番号。i == par[i]のとき、データiは木の根ノードである
  vector<int> par;
  // sizes[i]：根ノードiの木に含まれるデータの数。iが根ノードでない場合は無意味な値となる
  vector<int> sizes;

  UnionFind(int n) : par(n), sizes(n, 1) {
    // 最初は全てのデータiがグループiに存在するものとして初期化
    rep(i,n) par[i] = i;
  }

  // データxが属する木の根を得る
  int find(int x) {
    if (x == par[x]) return x;
    return par[x] = find(par[x]);  // 根を張り替えながら再帰的に根ノードを探す
  }

  // 2つのデータx, yが属する木をマージする
  void unite(int x, int y) {
    // データの根ノードを得る
    x = find(x);
    y = find(y);

    // 既に同じ木に属しているならマージしない
    if (x == y) return;

    // xの木がyの木より大きくなるようにする
    if (sizes[x] < sizes[y]) swap(x, y);

    // xがyの親になるように連結する
    par[y] = x;
    sizes[x] += sizes[y];
    // sizes[y] = 0;  // sizes[y]は無意味な値となるので0を入れておいてもよい
  }

  // 2つのデータx, yが属する木が同じならtrueを返す
  bool same(int x, int y) {
    return find(x) == find(y);
  }

  // データxが含まれる木の大きさを返す
  int size(int x) {
    return sizes[find(x)];
  }
};

クラスカル法の実装

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define rep(i,n) for (int i=0; i < int(n); i++)


// 素集合データ構造
struct UnionFind
{
  /* 略 */
};


// 頂点a, bをつなぐコストcostの（無向）辺
struct Edge
{
  int a, b, cost;

  // コストの大小で順序定義
  bool operator<(const Edge& o) const {
    return cost < o.cost;
  }
};

// 頂点数と辺集合の組として定義したグラフ
struct Graph
{
  int n;  // 頂点数
  vector<Edge> es;  // 辺集合

  // クラスカル法で無向最小全域木のコストの和を計算する
  // グラフが非連結のときは最小全域森のコストの和となる
  int kruskal() {
    // コストが小さい順にソート
    sort(es.begin(), es.end());

    UnionFind uf(n);
    int min_cost = 0;

    rep(ei, es.size()) {
      Edge& e = es[ei];
      if (!uf.same(e.a, e.b)) {
        // 辺を追加しても閉路ができないなら、その辺を採用する
        min_cost += e.cost;
        uf.unite(e.a, e.b);
      }
    }

    return min_cost;
  }
};

// 標準入力からグラフを読み込む
Graph input_graph() {
  Graph g;
  int m;
  cin >> g.n >> m;
  rep(i, m) {
    Edge e;
    cin >> e.a >> e.b >> e.cost;
    g.es.push_back(e);
  }
  return g;
}


int main()
{
  Graph g = input_graph();
  cout << "最小全域木のコスト: " << g.kruskal() << endl;
  return 0;
}

ここではグラフを辺集合として表現しています。 以前の説明（補足：グラフをプログラム上で管理する方法）では隣接行列と隣接リストのみしか説明していませんでしたが、クラスカル法のように辺全てをソートする場合にはこの表現方法のほうが効率的です。

入出力例は以下のようになります。 入力形式は基本的に以前の資料と同じです（ただし辺は無向とします）。

入力例：

5 8
0 1 10
0 3 5
1 2 1
1 3 1000
1 4 500
2 3 100
2 4 10000
3 4 5000

出力例：

最小全域木のコスト: 516

入力例のグラフは冒頭に挙げた最小全域木の例の図に対応します。

クラスカル法の計算量は、辺の数をEとするとO(E log E)になります。 Union Findの処理がほぼ定数時間であるため、最初に辺をソートする部分の計算時間が支配的になります。

問題

上2つの練習問題は上述のコードを貼るだけで解けます。 以下は最小全域木を使う自明でない問題です。

注意：グラフの連結性

この記事ではグラフは連結であることを仮定しています。 グラフが連結でない場合、クラスカル法で求まるものは連結成分数が最大の最小全域森となります。

余談：他の全域木問題

無向グラフの他の全域木問題も貪欲で解けるものが多いらしいです: 様々な全域木問題

有向グラフの最小全域木問題は無向グラフの場合ほど効率よく解くことができず、実装も難しいです（参考）。

余談：2012年度の講習会のページに新しい資料を作った理由

…という意思表示。